我们能预测未来吗?

来源:新原理研究所(ID:newprincipia)
制约宇宙的定律是否允许我们准确地预测到将来会有什么发生在我们身上?
“简短的回答即是否定的,也是肯定的。在原则上,定律允许我们预测未来。但在实践中,通常计算都太难了。”
——《十问:霍金沉思录》
1
我们能够预测未来吗?这是一个许多人都在试图回答的问题。
如果这个未来是之后的一秒,那么对我们周围的大多数事物来说,一秒并不会发生太多变化。
如果这个未来是接下来的一小时,我们可以非常确定地说,我们的房子还在,我们所在城市不会突然消失,我们会变得稍微老一点点。
如果这个未来是一天,我们仍然可以成功地预测一些事情。例如,火车时刻列表是一样的,这个世界还在。但有些事情却可能已经发生了很大的变化,比如股市可能在一天内崩盘了,一场风暴可能来袭。
如果这个未来是一个月,甚至一年,我们就会发现时间越久远,不确定性就越大。例如,你会相信一个月后的天气预报吗?你能精确地预测一年后的经济状况吗?
量子力学的奠基人之一玻尔(Niels Bohr)曾说过:“预测任何东西都是极其困难的,尤其是关于未来。”
能解释事物如何变化是我们预测事物的关键。变化往往是缓慢的,比如在生物学的进化系统,有时,变化又非常快,比如火山爆发。在某种意义上,两者都是可预测的事件。难以预测的是突然的变化——比如一个看似稳定的系统突然发生灾难性的变化。
这种重大的变化可能是由一个突然的外部因素引起的,也可能是由许多微弱的原因积累而致的。前者的例子有6500万年前因小行星撞击地球而导致的恐龙灭亡,后者的例子常被描述为是压垮骆驼的最后一根稻草,比如雪崩以及战争的爆发等等。
关于预测,有一个在哲学上似乎矛盾的问题,那就是:我们能否预测不可预测的事?
或许,数学能帮我们回答这个问题。
2
这个宇宙是全然随机的吗?还是说它具有某些秩序与模式?
很显然,大自然背后的确存在着基本的模式。正是因为意识到了这一点,人类才走上了通往现代化的道路,带来了科学的革命。可以说,科学所寻找的正是宇宙的秩序与模式。而数学不仅是这些模式的基础,它还为我们提供了一种描述宇宙的方法。
如果你仔细观察,你能看到在我们的周围充满了秩序与模式。例如雪花就是一个例子,虽然每一片雪花都不一样,但它们都有着精确的六倍对称。

自然界中遍布着高度规律的模式,我们早已习以为常,却鲜少停下来去思考它们为什么存在。然而,无论是雪花的形状,还是晶体的原子排列,又或是岩石的折叠,它们背后都有着非常?本而又了不起的成因。而更令人惊叹的是,一些伟大的头脑观察到了恒星和行星运动的秩序和模式,从而打开了通往现代世界的大门。
在这里,有一位不得不提到的科学家,那就是伽利略(Galileo Galilei)。1581年,伽利略在比萨大教堂中观察青铜吊灯的摆动时,他意识到吊灯的摆动是受可预测的规律支配的。他发现在气流影响下晃动的吊灯,无论其摆动的幅度为何,来回摆动一次所花的时间都是一样。然后,他用自己的脉搏来计时,在家里用大小不同但长度相同的钟摆来进行试验。最终证实了钟摆的摆动时间并不取决于它的大小,也不取决于它的位置,只取决于它的长度。
从此,钟摆的摆动成为了可预测的信息。不过当时的伽利略并不知道为什么会是这样,在他去世后不久,另一位伟大的科学家诞生了,那就是牛顿(Issac Newton)。
牛顿发现了许多隐藏在宇宙模式背后的定律,而且还发明了微积分等数学技术,这为我们理解宇宙的基本定律提供了重要工具。牛顿用他的三大运动定律清楚地描述了运动物体的运动方式。这些定律全部可以用数学来描述,特别是微分方程,可以精确地描述运动如何随时间演化。
利用微分方程在动力系统理论中所起的核心作用,最终可以得到钟摆的长度(l)与摆动周期(T)之间的精确数学关系:
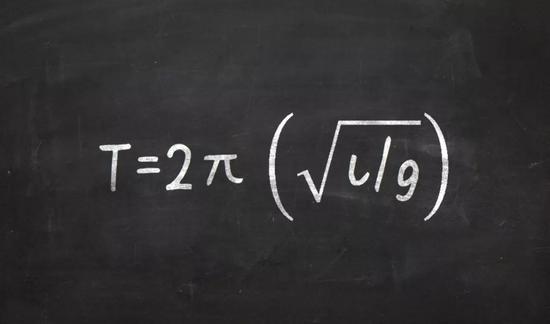
如果钟摆的长度l=1m,那么T=2.00607,其中g=9.81ms。
这与伽利略的观测完全吻合。
牛顿成功地将运动规律转化成了数学,然后用数学的解来预测系统在未来的行为。这为理解宇宙的一般方法提供了一个思路:
写下描述物理系统的数学方程,
解方程,
再用方程的解来预测未来。
这是一个真正的开创性想法,是科学发展史中转折性的时刻。
1781年,在赫歇尔(Herschel)发现天王星之后,利用牛顿的引力理论计算出了它的轨道。在此之前,天文学家已经用这种方法很完美地对其他行星的位置进行了预测。因此当他们发现牛顿理论的预测和天王星的位置之间存在一点小小的偏差时,他们非常震惊。
问题到底出在哪?数学家亚当斯(John Couch Adams)和勒威耶(Urbain le Verrier)推测可能存在另一颗行星影响了天王星的轨道。他们再次使用牛顿的理论,准确地预测出了这颗未知行星的位置。1846年,天文学家加勒(Galle)将望远镜对准了正确的方向,正如预测的那般,他发现了海王星的存在。
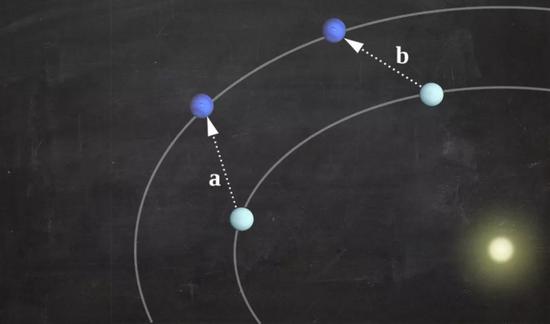
在数学的帮助下,天文学家发现了海王星。
这个巨大的胜利给了数学家们莫大的信心,这表明通过将观察到的宇宙模式转化成数学,就可以对未知事物的存在作出预测。到了1860年,麦克斯韦(John Clerk Maxwell)通过将法拉第(Faradays)的电和磁定律写成数学方程再求解之后,预言了电磁波的存在。
现在,我们预测未来天气也有着类似的工作原理,我们会利用当天的天气,然后求解纳维-斯托克斯大气运动方程和热力学方程以观察大气的演变。这些都是复杂性极高的方程,需要用计算机才可以求解。目前,我们已能够足够精确地完成这些计算,以较高的精度预测未来的天气。
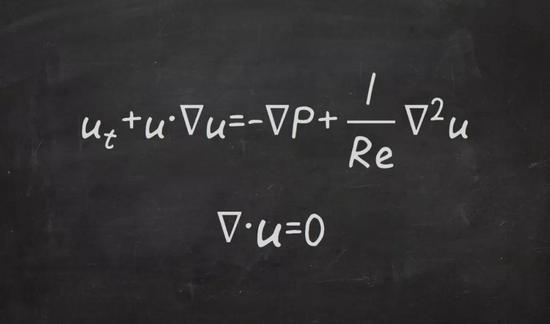
纳维-斯托克斯方程组。
在19世纪,人们认为宇宙是由服从牛顿定律的原子组成的,因此我们可以高度精确地预测原子的运动。法国数学家拉普拉斯(Pierre Simon Laplace)在1814年发表了一则大胆的声明,他说:
我们可以把宇宙现在的状态视为其过去的果以及未来的因。假如一位智者能知道在某一时刻所有促使自然运动的力和所有构成自然的物体的位置,假如他也能够对这些数据进行分析,那么在宇宙中,从最大的物体到最小的粒子,它们的运动都包含在一条简单的公式里。对于这位智者来说,没有任何事物会是含糊的,并且未来只会像过去般出现在他眼前。
这个智者被后人称为“拉普拉斯妖”。
拉普拉斯时代以来,宇宙在一个时刻的状态确定其他所有时间的状态的思想一直说是科学的中心信条。这意味着我们至少在原则上可以预测未来。。。。。。
——《十问:霍金沉思录》
我们很难把拉普拉斯的大胆预测以及拉普拉斯妖与我们所观察到的现实世界相提并论,因为对人类而言,许多事件都是不可预测的。事实上,人类的行为本质上是不可预测的,我们能够行使自由意志。
不可预测也发生在物质世界。比如我们无法准确预测10天之后的天气,同样我们也很难预测气候现象,厄尔尼诺南方涛动现象(ENSO)就是一个很好的例子。
不可预测性的无处不在似乎与拉普拉斯预测的有序宇宙相矛盾。伴随着牛顿定律在预测未来方面上的许多成功案例,我们不禁要问这样一个问题:
我们在自然界中看到的许多不可预测性真的是因为自然界的复杂性和无法解释性导致的吗?还是说,看似不可预测的行为实际上能从受牛顿定律支配的系统中产生?
3
我们可以通过一个相对简单的系统来回答这个问题,那就是双摆系统。双摆系统是由两个单摆耦合在一起形成的,它是伽利略对单摆研究的延伸,显然,这个系统也受牛顿运动定律的支配。
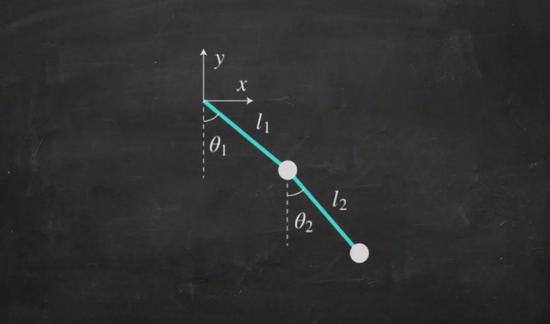
这个系统只有两个运动的部分,即上半部分的单摆和底部的单摆,每个部分都有位置和角速度这两个变量。因此这个系统可以简化为4个自由度。这比有着数十亿个自由度的天气要少得多。但即便如此,双摆的行为仍然非常复杂,我们可以将它的运动划分为三类。
如果上半部分和下半部分的单摆以较小的角度被拉到同一边(下图左),那么它们会像单摆一样以规律的方式同步摆动,如果这两个部分以较小的角度被拉向相反的方向(下图右),那么当它们被释放时则会继续朝着相反的方向运动,这种异相的运动会一直周期性地持续下去。

最后,如果我们给钟摆一个大大的摆动,那么双摆将以一种最不稳定的几乎随机的方式运动。下图所示的就是这样一个例子,一盏灯被连接到了双摆最低的部分,图中记录的便是它在这种情况下它随时间的运动轨迹。不难看出,它的运动不仅复杂,而且极难预测。这样的运动已经完全不符合我们前面所描述的可预测性,而是成为了混沌运动。

可能有人会说这种混沌运动之所以看似随机,是因为双摆只是对随机气流做出反应。然而事实却并非如此。根据牛顿运动定律,我们可以用一对耦合的非线性二阶常微分方程来描述这样一个双摆系统的运动:
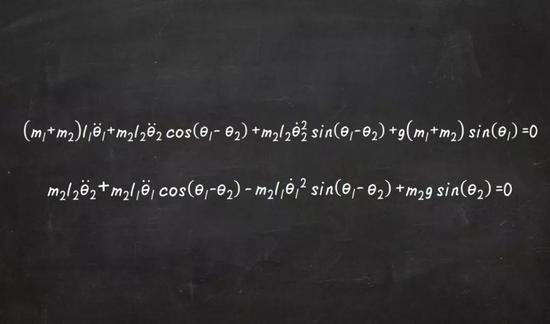
θ:角度,l:长度,m:质量。
如果夹角较小,则可以用线性逼近,对系统进行精确求解,预测上述的同相和异相行为。但如果夹角很大,则只能使用计算机来进行数值求解了。在完全基于牛顿运动定律的基础上,计算机可以给出与物理系统完全相同的行为,这表明混沌行为确实可以作为牛顿方程的解存在。
那么我们应该如何定义混沌行为呢?数学家Chris Budd将其描述为:
混沌运动是一种复杂,不规则且不可预测的行为,它产生于一个“简单”的系统,可以用“简单”的数学定律进行精确描述。
混沌运动的一个关键特征在于它们对初始条件的敏感性,两个非常接近的初始状态会以非常不同的方式进化,然后产生混沌。这种现象有一个通俗易懂的名字——蝴蝶效应。蝴蝶效应的概念引发了公众的无限想象,它表明即使是微小的变化也会对未来产生巨大的影响,这种观点似乎能与我们对宇宙如何运行的一些看法产生共鸣。
这种混沌行为存在于许多物理系统中。比如一张混乱的台球桌,台球在桌子上撞来撞去,它们的运动模式是高度复杂的,然而,就像双摆一样,它产生于非常简单的运动定律。
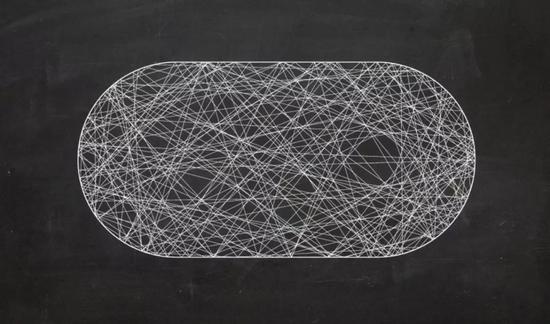
这个场景在光学,声学以及高频WiFi中都有非常实际的应用。就拿WiFi来说,上图中的线就对应于电磁辐射射线。这张复杂非凡的图片意味着真正的混沌行为无处不在,我们很难预测一个房间内的WiFi覆盖强度。
…… 然而,在实践中,我们预测未来的能力受限于方程的复杂性以及它们通常具有称为混沌的属性这一事实。
——《十问:霍金沉思录》
4
混沌理论起源于洛伦兹(E。 Lorenz)在1963年发表的一篇论文,当时他正在试图研究大气的运动。经过大量简化之后,他将系统简化为三个常微分方程:
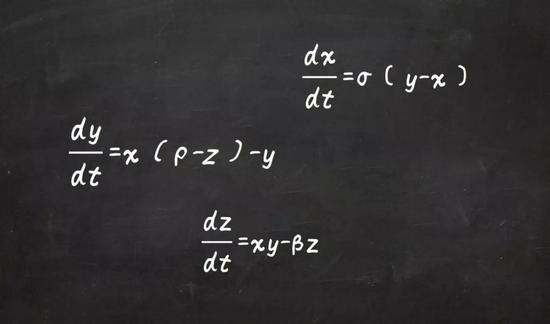
在20世纪60年代以前,要准确地解出这个方程组是不可能的。但之后快速数字计算机的出现,使求解成为可能,其结果让洛伦兹非常惊讶。他得到的结果并没有出现他以为会出现的周期行为,而是以一种不稳定的方式出现,他称之为混沌。
下图显示的是用一组具有气象意义的固定参数所绘制的x(t)演化图,图中显示了随着时间的推移具有复杂轨迹的混沌行为。这张图采用了x(0)的两个稍微不同的初始条件(图中用黄线和蓝线表示),在 t=24 时,它们的轨迹都非常接近,但在 t=24 之后,它们开始出现显著的差异。
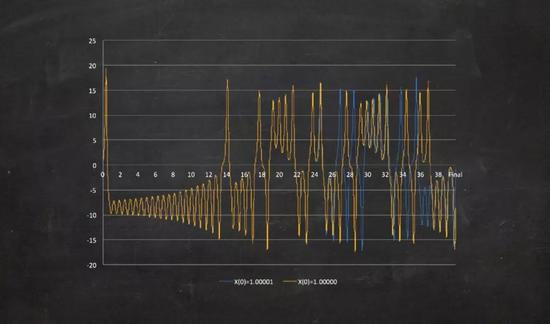
将x(t)和y(t)绘制在一起更能说明问题。在下图中,点(x, y)围绕一个蝴蝶形状的集合运动。这个集合被称为奇异吸引子,因为它能吸引所有的轨迹,但它既不是周期性的,也不是一个定点。虽然吸引子周围的点都是混沌的,但吸引子本身的形状却是确定的。奇异吸引子本身具有良好的结构,它是分形集的一个例子。
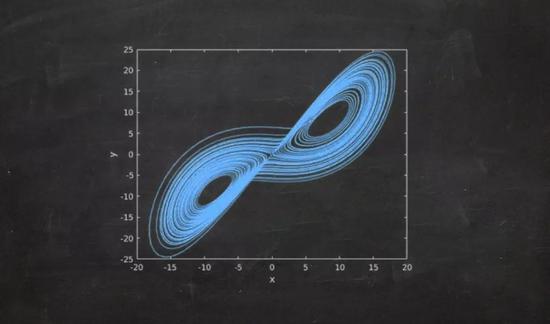
上世纪60年代发现的混沌在当时引发了很大的轰动,它吸引了许多学者的关注,也掀起了大众媒体对此的报道热情,其中还包括大量的炒作。不过,混沌动力学的发现其实发生在更早的时候,它的发现很大程度上要归功于伟大的法国数学家庞加莱(Henri Poincare)。
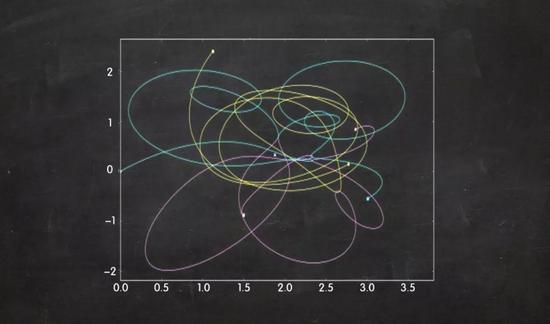
当时,庞加莱正在研究太阳系的稳定性。我们知道,如果一颗行星绕着太阳旋转,那么它的运动是周期性的,而且可以用牛顿定律精确地预测出来。然而,庞加莱证明了一个由三个质量相似的物体组成的系统在万有引力作用下只会在不规则轨道上运动。


5
我们很难看出洛伦兹系统中的混沌行为是如何产生的,因此我们可以研究一个更为简单的系统,它也具有类似的混沌行为,那就是著名的逻辑斯谛映射(Logistic Map)。假设我们要预测一个城镇从一年到来年的人口,我们设xn为这个城镇在未来第n年的人口数,也就是说 n=0 为已知的当前年份的城镇人口数(x0)。
1798年,马尔萨斯(Malthus)在《人口原理》一文中提出了一个简单的人口增长模型。他假设,任何一年的出生人口比例是固定的,死亡人口比例也是固定的。这意味着在n+1年的人口将与n年的人口成比例:
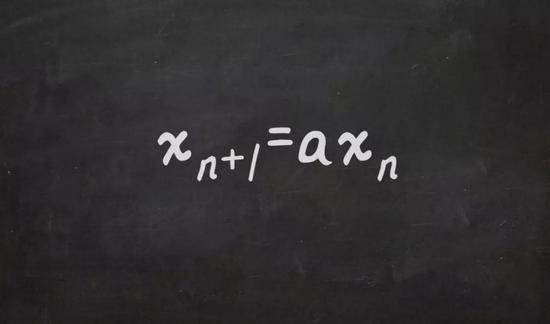
这是一个离散动力系统的例子。在这种情况下,马尔萨斯模型给出了简单且可预测的解:
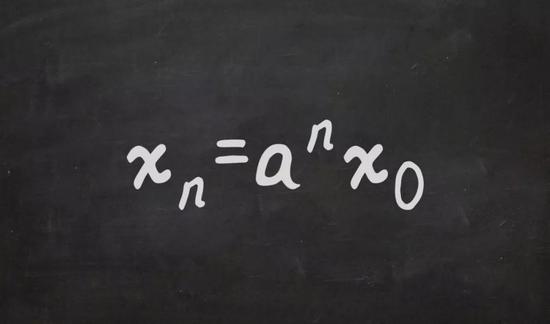
如果 a<1,则人口数量减少,如果 a=1,人口数量保持不变,如果 a>1,则人口数量呈现无限制地增长,即所谓的马尔萨斯增长。马尔萨斯本人也意识到这是种不现实的模型,因为人口最终会耗尽资源,然后开始下降。一种解决方法是引入人口的上限M,以便将资源的有限程度纳入考量,于是修正过的马尔萨斯模型变成了:

将以上等式稍做变形,便得到了著名的人口增长逻辑斯谛映射模型:

下图所示的是 2.4<r<4 的逻辑斯谛映射图。从这个图中我们可以清楚地看到当 r<3 时存在一个固定的点,在r趋近于3的时候,一个点变成了两个点的双循环,当 r>3.56995 时,混沌行为出现了。不过在 r=3.828 附近也存在一个稳定的三循环。数学家一直在为了更好地理解这张图而努力。
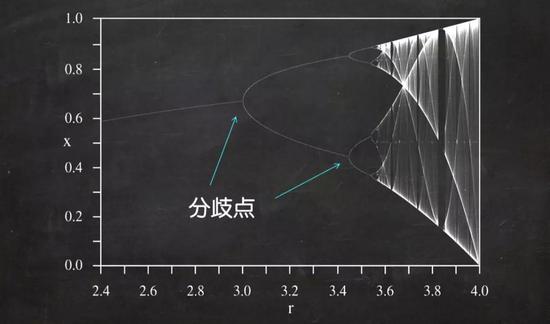
动力系统其实就是一个会随时间演化的系统,它可以由一个状态向量x(t)描述。它可以是一个连续的时间函数(如双摆系统),江绵康简历也可以是离散时间的函数(如逻辑斯谛映射)。随着动力系统的参数发生变化,它的状态也会发生变化。一个状态可以被创造,可以消失,可以失去它的稳定性,也可以变成另一种状态,就如我们在逻辑斯谛映射图中所看到的那样。
我们常听人说到“压死骆驼的最后一根稻草”这句话,其实在这个场景下,骆驼——或者更确切地说是骆驼的背部,就是一个动力学系统的解,这个系统的参数是它背上的稻草量。如果稻草的量少,那么驼背就是这个动力系统的一个稳定的固定点。但在随着加载参数逼近临界值,固定点变得不再稳定,其结果就是导致驼背断裂。
在这里,我们看到了一个临界点,超过这个临界点,控制这个系统的参数发生的一点微小的变化就能导致系统最终状态出现一个不可逆的巨大变化。数学家已经对这些状态的转换进行了非常详细的研究,它们可以用“分歧理论”来解释。就如上图所示的逻辑斯谛映射图中出现的分歧点就显示了许多与其相关的特征,包括著名的“通往混沌的周期倍增路线”。
6
混沌理论有用吗?
没错,许多数学理论在一开始时都很抽象,你很难想象它的用途,但它们却能在后来成为科学和技术的核心。?沌理论就是很好的例子。洛伦兹在20世纪60年代的工作在很大程度上都是理论性的,但人们很快意识到,许多物理系统确实有非常?沌的行为。许多其他重要系统也被认为是混沌的,比如天气,汽车尾气,电力供应系统,摩擦刹车,气候变化,WiFi,脑电图信号,心电图信号以及小行星的运动等等。?沌理论使我们能够理解,测量,并在某些情况下控制这些混沌系统表现出的不确定性行为。
现在我们认识到,混沌行为是由复杂的,非线性的,确定性过程控制的任何事物的自然模式的一部分。小行星就是一个很好的例子,它们有着非常复杂的轨道,这是我们必须理解的事实,否则我们可能无法预测小行星是否以及何时会撞击地球。从这个角度看,混沌理论在拯救人类方面还具有至关重要的意义!
当然混沌还有一些不这么耸人听闻的应用。例如,混沌理论在计算机图形学中扮演着越来越重要的作用。?沌理论几乎有着无限的应用,江绵康简历虽然它带来的似乎是混乱和不可预测性,但它却是我们理解世界的一种至关重要的方法。





